

In this case, the domain of f consists of all real numbers except −3 and 7, and the domain of g consists of all real numbers except 7 and −7. ( f / g ) ( x ) = f ( x ) ÷ g ( x ) = 2 x 2 + 13 x − 7 x 2 − 4 x − 21 ÷ 2 x 2 + 5 x − 3 49 − x 2 = 2 x 2 + 13 x − 7 x 2 − 4 x − 21 ⋅ 49 − x 2 2 x 2 + 5 x − 3 M u l t i p l y b y t h e r e c i p r o c a l o f t h e d i v i s o r. Given f ( x ) = 2 x 2 + 13 x − 7 x 2 − 4 x − 21 and g ( x ) = 2 x 2 + 5 x − 3 49 − x 2, find ( f / g ) ( x ) and determine the restrictions. The restrictions to the domain of a quotient will consist of the restrictions of each function as well as the restrictions on the reciprocal of the divisor. In general, given polynomials P, Q, R, and S, where Q ≠ 0, R ≠ 0, and S ≠ 0, we have Dividing rational expressions is performed in a similar manner. To divide two fractions, we multiply by the reciprocal of the divisor. Multiply the functions and then simplify the result. Therefore, the domain of the product consists of all real numbers except 5 and − 5 3. In this case, the domain of f consists of all real numbers except 5, and the domain of g consists of all real numbers except − 5 3. Given f ( x ) = 9 x 2 − 25 x − 5 and g ( x ) = x 2 − 2 x − 15 3 x + 5, find ( f ⋅ g ) ( x ) and determine the restrictions to the domain. Generally, negative denominators are avoided. In other words, a negative fraction is shown by placing the negative sign in either the numerator, in front of the fraction bar, or in the denominator. − ( a − b ) = ( b − a ) or b − a a − b = − 1 ( a + b ) = ( b + a ) or b + a a + b = 1 This is the case because addition is commutative. Care should be taken not to confuse this with the fact that ( a + b ) = ( b + a ). This leads us to the opposite binomial property If given a binomial a − b, then the opposite is − ( a − b ) = b − a. For example, the opposite of the polynomial ( x − 3 ) is written as Finding the opposite of a polynomial requires the application of the distributive property. We define the opposite of a polynomial P to be − P. With this understanding, we can cancel any common factors.į ( x ) = ( 2 x − 1 ) ( x + 3 ) ( 2 x + 1 ) ( 2 x − 1 ) = x + 3 2 x + 1Īnswer: f ( x ) = x + 3 2 x + 1, where x ≠ ± 1 2 To find the restrictions, first set the denominator equal to zero and then solve įirst, factor the numerator and denominator.į ( x ) = 2 x 2 + 5 x − 3 4 x 2 − 1 = ( 2 x − 1 ) ( x + 3 ) ( 2 x + 1 ) ( 2 x − 1 )Īny x-value that makes the denominator zero is a restriction.

State the restrictions and simplify: f ( x ) = 2 x 2 + 5 x − 3 4 x 2 − 1. Once the restrictions are determined we can cancel factors and obtain an equivalent function as follows: The restrictions to the domain of a rational function are determined by the denominator. S e t - b u i l d e r n o t a t i o n I n t e r v a l n o t a t i o n ( − ∞, 2 ) ∪ ( 2, 3 ) ∪ ( 3, ∞ )
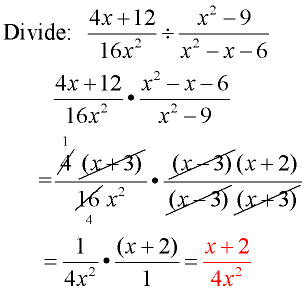
We can express its domain using notation as follows: Therefore, the original function is defined for any real number except 2 and 3. Set each factor in the denominator equal to 0 and solve. To do this, apply the zero-product property. For example, consider the functionį ( x ) = ( x − 1 ) ( x − 3 ) ( x − 2 ) ( x − 3 )īecause rational expressions are undefined when the denominator is 0, we wish to find the values for x that make it 0. We often express the domain of a rational function in terms of its restrictions. are the real numbers for which the expression is not defined. Restrictions The set of real numbers for which a rational function is not defined. consists of all real numbers x except those where the denominator q ( x ) = 0. The domain of a rational function The set of real numbers for which the rational function is defined. Where p ( x ) and q ( x ) are polynomials and q ( x ) ≠ 0.

Rational functions Functions of the form r ( x ) = p ( x ) q ( x ), where p ( x ) and q ( x ) are polynomials and q ( x ) ≠ 0. Identifying Restrictions and Simplifying Rational Functions


 0 kommentar(er)
0 kommentar(er)
